Como mecanismo de transmisión, el engranaje planetario se usa ampliamente en diversas prácticas de ingeniería, como reductores de engranajes, grúas, reductores de engranajes planetarios, etc. Para los reductores de engranajes planetarios, puede reemplazar el mecanismo de transmisión del tren de engranajes de eje fijo en muchos casos. Debido a que el proceso de transmisión de engranajes es contacto de línea, el engrane prolongado causará fallas en el engranaje, por lo que es necesario simular su resistencia. Li Hongli et al. utilizó el método de engrane automático para engranar el engranaje planetario y obtuvo que el torque y la tensión máxima son lineales. Wang Yanjun et al. también engranó el engranaje planetario mediante el método de generación automática y simuló la simulación estática y modal del engranaje planetario. En este documento, se utilizan principalmente elementos tetraédricos y hexaédricos para dividir el engrane, y se analizan los resultados finales para ver si se cumplen las condiciones de resistencia.

1、 Establecimiento del modelo y análisis de resultados

Modelado tridimensional de engranajes planetarios

Engranaje planetarioSe compone principalmente de corona dentada, engranaje solar y engranaje planetario. Los principales parámetros seleccionados en este trabajo son: 66 dientes de la corona dentada interior, 36 dientes del engranaje solar, 15 dientes del engranaje planetario, 150 mm de diámetro exterior de la corona dentada interior, 2 mm de módulo, 20° de ángulo de presión, 20 mm de ancho de diente, 1 coeficiente de altura de la adenda, 0,25 de coeficiente de holgura y tres engranajes planetarios.

Análisis de simulación estática de engranajes planetarios

Definir las propiedades del material: importar el sistema de engranajes planetarios tridimensionales dibujado en el software UG a ANSYS y configurar los parámetros del material, como se muestra en la Tabla 1 a continuación:

Mallado: La malla de elementos finitos se divide en tetraedros y hexaedros, y el tamaño básico del elemento es de 5 mm. Dado queengranaje planetarioEl engranaje solar y el anillo interior del engranaje están en contacto y engranan. La malla de las piezas de contacto y de malla está densificada y su tamaño es de 2 mm. Primero, se utilizan rejillas tetraédricas, como se muestra en la Figura 1, generando un total de 105906 elementos y 177893 nodos. Posteriormente, se adopta una rejilla hexaédrica, como se muestra en la Figura 2, generando un total de 26957 celdas y 140560 nodos.

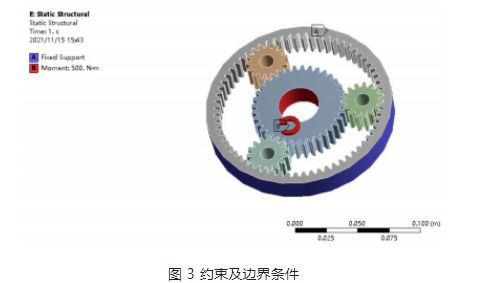
Aplicación de carga y condiciones de contorno: Según las características de funcionamiento del engranaje planetario en el reductor, el engranaje solar es el engranaje impulsor, el engranaje planetario es el engranaje impulsado y la salida final se realiza a través del portaplanetarios. Fije el anillo interior del engranaje en ANSYS y aplique un par de 500 N·m al engranaje solar, como se muestra en la Figura 3.

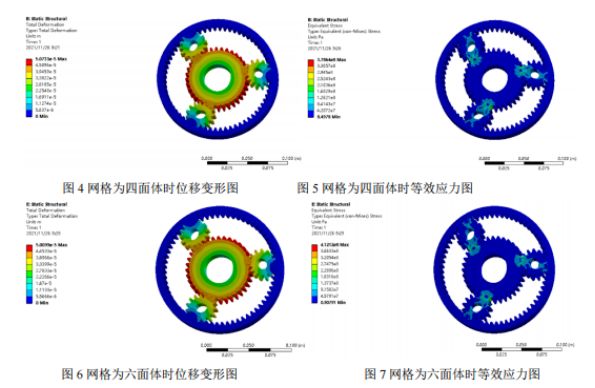
Posprocesamiento y análisis de resultados: A continuación, se presentan el nefograma de desplazamiento y el nefograma de tensión equivalente del análisis estático obtenidos a partir de dos divisiones de la malla, y se realiza un análisis comparativo. A partir del nefograma de desplazamiento de los dos tipos de malla, se observa que el desplazamiento máximo se produce en la posición donde el engranaje solar no engrana con el engranaje planetario, y la tensión máxima se produce en la raíz del engrane del engranaje. La tensión máxima de la malla tetraédrica es de 378 MPa y la de la malla hexaédrica es de 412 MPa. Dado que el límite elástico del material es de 785 MPa y el factor de seguridad es de 1,5, la tensión admisible es de 523 MPa. La tensión máxima de ambos resultados es inferior a la admisible, y ambos cumplen las condiciones de resistencia.

2、 Conclusión

A través de la simulación por elementos finitos del engranaje planetario, se obtienen el nefograma de deformación por desplazamiento y el nefograma de esfuerzos equivalentes del sistema de engranajes, de los cuales se obtienen los datos máximos y mínimos y su distribución en elengranaje planetarioSe puede encontrar el modelo. La ubicación de la tensión equivalente máxima es también el punto donde los dientes del engranaje tienen mayor probabilidad de fallar, por lo que se debe prestar especial atención a este punto durante el diseño y la fabricación. Mediante el análisis de todo el sistema de engranajes planetarios, se supera el error causado por el análisis de un solo diente.